Rethinking Test-time Alignment for Language Models

Language models can already be aligned to human preferences through reinforcement learning from human feedback (RLHF), but this process depends on finetuning — a step that is often inaccessible for practical or proprietary reasons. When model weights are closed, or when training compute is limited, we need other ways to adjust model behavior.

One promising direction is to use additional computation at inference. Instead of retraining, we spend more time reasoning, sampling, or evaluating outputs. In principle, more compute should yield better results: the model explores multiple trajectories and selects one that aligns best with human preference (best-of-n).

In practice, this approach runs into a familiar failure mode. Current test-time search methods rely on reward models to evaluate candidate generations, yet these reward models are imperfect. As the search process expands, it begins to over-optimize the reward signal, producing text that satisfies the model's scoring function but not the underlying preference it was meant to represent. Performance degrades exactly when it should be improving.

The animation below shows how this plays out on a simple riddle task.

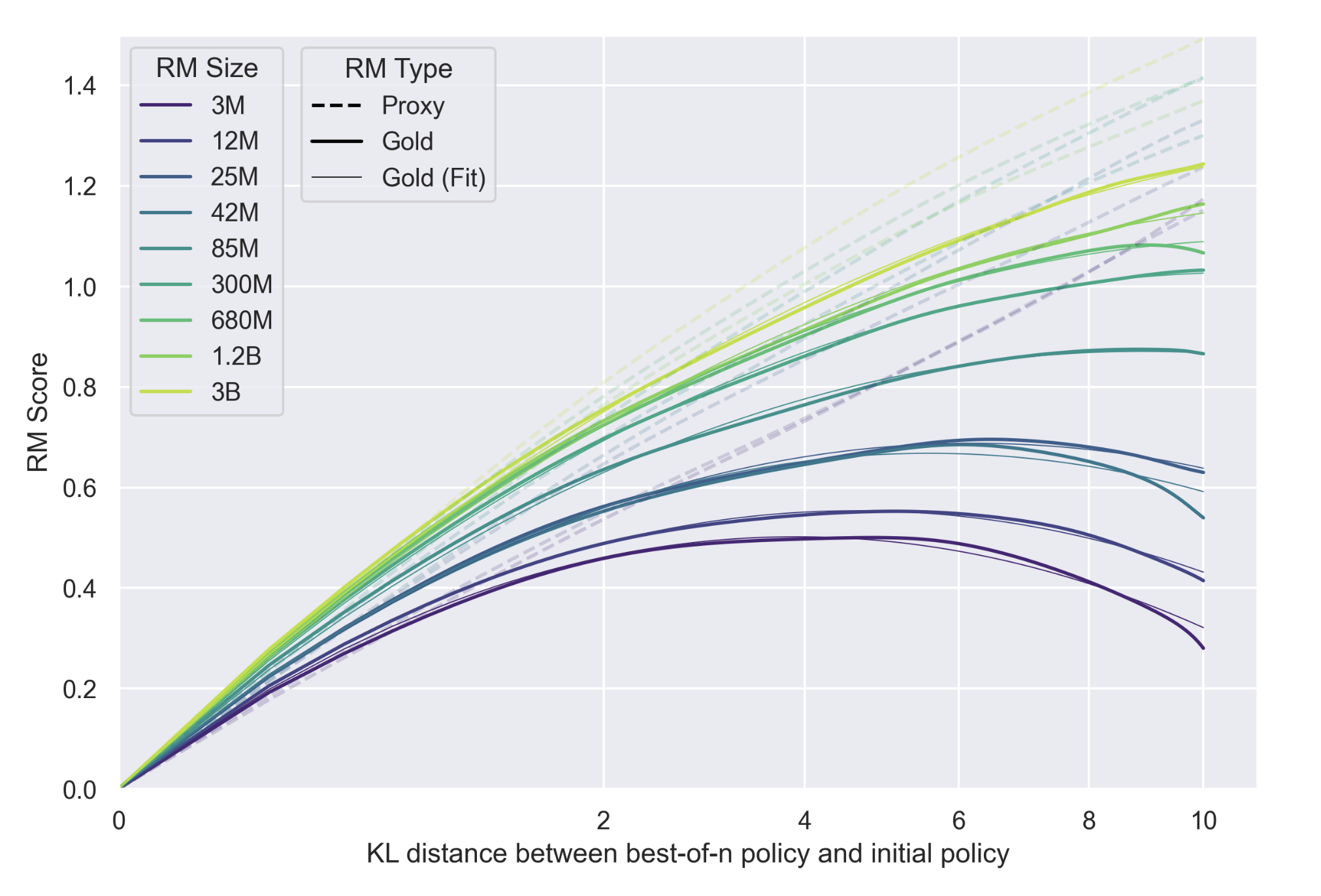
This pattern isn't unique to a single example. The same dynamic appears systematically when we scale up search or reward model capacity. In the figure below, adapted from Gao et al. (2022), we plot reward-model ("proxy") and human-preference ("gold") scores as a function of the KL distance between a best-of-n policy and its base model.

We address this problem with QAlign, a test-time alignment method that treats the reward model not as a target to maximize, but as a guide for sampling from an aligned distribution. The method draws from recent work on Markov chain Monte Carlo (MCMC) text generation (QUEST). Rather than searching for the single best sequence, it constructs a chain of samples that gradually converges toward the distribution implied by the reward model. This process produces better-aligned generations as compute increases, without altering model parameters or requiring access to logits.

When applied with a reward model trained on the Tülu 3 preference dataset, QAlign outperforms several existing test-time methods—best-of-n, majority voting, and weighted majority voting—and even surpasses finetuned baselines such as Direct Preference Optimization (DPO) across benchmarks including GSM8K, MATH500, MMLU-Redux, IFEval, and TruthfulQA.

By converting test-time compute into alignment capability, QAlign extends what can be achieved with existing language models, offering a practical route to improved behavior without retraining.

Language Model Alignment

At its core, aligning a language model means updating its beliefs about which responses people actually prefer. We can think of this as a kind of Bayesian inference.

A pretrained model, $p_{\text{LM}}(y \mid x)$, gives us a prior over possible responses $y$ for a prompt $x$. A reward model $r(y,x)$, trained from human preferences, acts like new evidence. Combining the two defines an ideal posterior distribution over aligned outputs:

$$\pi(y \mid x) \propto p_{\text{LM}}(y \mid x) \, \exp\left(\frac{r(y, x)}{\beta}\right).$$

In principle, sampling from this posterior would give us perfectly aligned responses. In practice, it's intractable — we can't compute the partition function or sample exactly from such a vast space of possible texts.

Most current alignment methods approximate this posterior indirectly. They introduce a new model $q_\theta(y \mid x)$, initialized from the base LM, and train it to match the ideal distribution by maximizing expected reward while staying close to the original model. This gives rise to the familiar RLHF objective, which balances two forces: one pushing toward higher reward, the other keeping the model's behavior within a reasonable KL distance from the base policy.

Methods like PPO, DPO, and related algorithms optimize this objective efficiently, but all share a common structure — they produce a single aligned model through expensive finetuning. The process requires gradient access, large compute budgets, and fixed assumptions about what "aligned" means. Once trained, the model is frozen.

Test-Time Alignment via MCMC

Casting alignment as Bayesian inference helps separate what we want from how we try to get it. In the previous section, we saw that traditional approaches approximate the aligned posterior distribution by training a new model $q_\theta(y \mid x)$. This has clear advantages — once trained, the model can generate aligned outputs in a single forward pass — but it also has some drawbacks.

First, finetuning is expensive. Each round of alignment means retraining billions of parameters. Second, many of today's best models—GPT-4, Gemini, Claude—don't even expose their weights. Third, because the approximation is learned once and amortized across all prompts, the model's alignment is necessarily an average. It does well on typical prompts but may deviate significantly on any specific one. Finally, this process bakes in a single notion of "human preference." Real users and contexts are more diverse than any single reward model can capture.

These limitations point to a more flexible idea: test-time alignment. Instead of training a new model, we can improve alignment dynamically by spending more compute on a single prompt. In other words, use extra inference steps to locally approximate the ideal aligned distribution $\pi(y \mid x)$.

Sampling toward the aligned distribution

Our goal is to draw samples from

$$\pi_\beta(y \mid x) \propto p_{\text{LM}}(y \mid x) \exp\left(\frac{r(y, x)}{\beta}\right),$$

the same target introduced earlier. MCMC provides a principled way to do this: build a Markov chain whose equilibrium distribution is exactly $\pi_\beta(y \mid x)$.

We start with an initial guess $y_0 \sim p_{\text{LM}}(y \mid x)$. At each step $t$, we propose a small edit $y$ using a proposal distribution $q(y \mid y_t, x)$ and decide whether to accept it based on how much better it scores under the reward model.

Following the approach of QUEST \citep{quest}, we define our proposal by re-sampling a random suffix of the sequence from the base LM:

$$q(y \mid y_t, x, i) = p_{\text{LM}}(y_{i:N} \mid y_{\lt i}^t, x)\;\; \mathbf{1}[y_{1:i} = y_{1:i}^t]$$

The acceptance step uses the standard Metropolis–Hastings criterion:

$$\alpha_\beta(y, y_t) = \min\left\{1, \exp\left(\frac{r(x, y) - r(x, y_t)}{\beta}\right) \frac{|y_t|}{|y|}\right\}.$$

If accepted, we set $y_{t+1} = y$; otherwise, we keep the previous sample. Repeating this process produces a sequence $(y_0, y_1, \ldots, y_T)$ that converges to the aligned distribution $\pi_\beta(y \mid x)$. Each additional step refines the approximation — more compute means a better estimate.